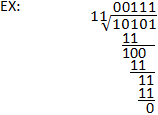二进制计算器

* and,or,not,xor 运算限制为32位数字

二进制转换器 ►

二进制加法

二进制加法遵循与十进制系统中的加法相同的规则，不同之处在于，当加法值等于 10 时，不会发生 1，而是在加法结果等于 2 时发生结转。有关说明，请参阅下面的示例。

请注意，在二进制系统中：

0 + 0 = 0
0 + 1 = 1
1 + 0 =
1 1 + 1 = 0，结转 1，即 10

例如：

		10	11	11	10	1
+		1	0	1	1	1
=	1	0	0	1	0	0

二进制加法和十进制加法之间唯一真正的区别是二进制系统中的值 2 相当于十进制系统中的值 10。请注意，上标 1 表示被传递过来的数字。进行二进制加法时需要注意的一个常见错误是，1 + 1 = 0 也有一个从前一列延续到其右侧的 1。然后，底部的值应为 1，而不是 0。这可以在上面示例中右侧的第三列中观察到。

二进制减法

与二进制加法类似，二进制和十进制减法之间几乎没有区别，除了仅使用数字 0 和 1 引起的减法。在减去的数字大于从中减去的数字的任何情况下，都会发生借用。在二元减法中，唯一需要借用的情况是从 0 中减去 1。发生这种情况时，借用列中的 0 实质上变为“2”（将 0-1 更改为 2-1 = 1），同时将借用列中的 1 减少 1。如果以下列也为 0，则必须从每个后续列中进行借用，直到值为 1 的列可以减小到 0。有关说明，请参阅下面的示例。

请注意，在二进制系统中：

0 - 0 = 0
0 - 1 = 1，借用 1，导致 -1 结转超过
1 - 0 = 1
1 - 1 = 0

例子 1：

		-11	20	1	1	1
–		0	1	1	0	1
=		0	1	0	1	0

例子 2：

		-11	2-10	0
–		0	1	1
=		0	0	1

请注意，显示的上标是借用时每个位发生的变化。借用列实质上从借用中获得 2，从中借用的列减少 1。

二进制乘法

二进制乘法可以说比十进制对应物更简单。由于仅使用的值为 0 和 1，因此必须添加的结果要么与第一项相同，要么为 0。请注意，在每个后续行中，需要添加占位符 0，并且值向左移动，就像在十进制乘法中一样。二进制乘法的复杂性源于繁琐的二进制加法，这取决于每个项中有多少位。有关说明，请参阅下面的示例。

请注意，在二进制系统中：

0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1

例如：

			1	0	1	1	1
×						1	1
			1	0	1	1	1
+		1	0	1	1	1	0
=	1	0	0	0	1	0	1

从上面的例子中可以看出，二进制乘法的过程与十进制乘法的过程相同。请注意，0 占位符写在第二行中。通常，0 占位符在十进制乘法中不直观地存在。虽然在此示例中可以执行相同的操作（假设为 0 占位符而不是显式占位符），但此示例中包含它，因为 0 与任何二进制加法/减法计算器相关，如本页提供的计算器。如果不显示 0，则在添加上面显示的二进制值时可能会犯排除 0 的错误。再次注意，在二进制系统中，1 右侧的任何 0 都是相关的，而值中最后一个 1 左侧的任何 0 都不是相关的。

例如：

1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 0 0
≠ 1 0 1 0 1 0 0 0 0 0 0

二进制除法

二进制除法的过程类似于十进制系统中的长除法。仍然以相同的方式除以除数，唯一显着的区别是使用二进制而不是十进制减法。请注意，对二进制减法的良好理解对于进行二进制除法非常重要。 请参阅下面的示例以及二进制减法部分进行说明。